¿Qué son los axiomas de probabilidad?

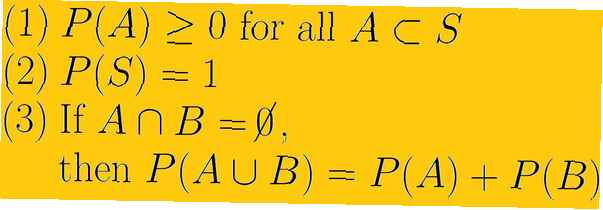
Una estrategia en matemáticas es comenzar con unas pocas declaraciones, luego construir más matemáticas a partir de estas declaraciones. Las declaraciones iniciales se conocen como axiomas. Un axioma es típicamente algo que es matemáticamente evidente. De una lista relativamente corta de axiomas, la lógica deductiva se usa para probar otras declaraciones, llamadas teoremas o proposiciones.

El área de las matemáticas conocida como probabilidad no es diferente. La probabilidad puede reducirse a tres axiomas. Esto fue hecho por el matemático Andrei Kolmogorov. El puñado de axiomas que son probabilidad subyacente se puede utilizar para deducir todo tipo de resultados. ¿Pero cuáles son estos axiomas de probabilidad??

Definiciones y preliminares

Para entender los axiomas de probabilidad, primero debemos discutir algunas definiciones básicas. Suponemos que tenemos un conjunto de resultados llamado espacio muestral S. Este espacio muestral puede considerarse como el conjunto universal para la situación que estamos estudiando. El espacio muestral se compone de subconjuntos llamados eventos. mi₁, mi₂,... , mi_norte. 

También asumimos que hay una manera de asignar una probabilidad a cualquier evento mi. Esto se puede considerar como una función que tiene un conjunto para una entrada y un número real como salida. La probabilidad del evento. mi se denota por PAG(mi).

Axioma Uno

El primer axioma de probabilidad es que la probabilidad de cualquier evento es un número real no negativo. Esto significa que lo más pequeño que una probabilidad puede ser es cero y que no puede ser infinito. El conjunto de números que podemos usar son números reales. Esto se refiere tanto a números racionales, también conocidos como fracciones, como a números irracionales que no se pueden escribir como fracciones..

Una cosa a tener en cuenta es que este axioma no dice nada acerca de cuán grande puede ser la probabilidad de un evento. El axioma elimina la posibilidad de probabilidades negativas. Refleja la noción de que la probabilidad más pequeña, reservada para eventos imposibles, es cero.

Axioma dos

El segundo axioma de probabilidad es que la probabilidad de todo el espacio muestral es uno. Simbólicamente escribimos PAG(S) = 1. Implícito en este axioma está la noción de que el espacio muestral es todo lo posible para nuestro experimento de probabilidad y que no hay eventos fuera del espacio muestral.

Por sí mismo, este axioma no establece un límite superior en las probabilidades de eventos que no son todo el espacio muestral. Refleja que algo con absoluta certeza tiene una probabilidad del 100%.

Axioma Tres

El tercer axioma de probabilidad trata con eventos mutuamente excluyentes. Si mi₁ y mi₂ son mutuamente excluyentes, lo que significa que tienen una intersección vacía y usamos U para denotar la unión, luego PAG(mi₁ U mi₂ ) = PAG(mi₁) + PAG(mi₂).

El axioma en realidad cubre la situación con varios eventos (incluso contablemente infinitos), cada par de los cuales son mutuamente excluyentes. Mientras esto ocurra, la probabilidad de la unión de los eventos es la misma que la suma de las probabilidades:

PAG(mi₁ U mi₂ U ... U mi_norte ) = PAG(mi₁) + PAG(mi₂) + ... + mi_norte

Aunque este tercer axioma podría no parecer tan útil, veremos que combinado con los otros dos axiomas es bastante poderoso..

Aplicaciones de Axiom

Los tres axiomas establecen un límite superior para la probabilidad de cualquier evento. Denotamos el complemento del evento. mi por mi^C. De la teoría de conjuntos, mi y mi^C tienen una intersección vacía y son mutuamente excluyentes. además mi U mi^C = S, todo el espacio muestral.

Estos hechos, combinados con los axiomas nos dan: