Teoría de conjuntos

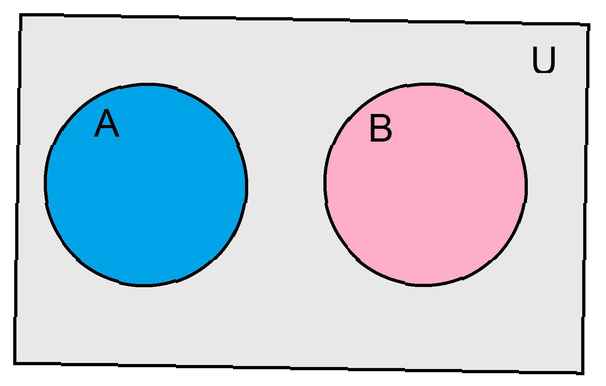
La teoría de conjuntos es un concepto fundamental en todas las matemáticas. Esta rama de las matemáticas forma una base para otros temas.. 

Intuitivamente, un conjunto es una colección de objetos, que se denominan elementos. Aunque esto parece una idea simple, tiene algunas consecuencias de largo alcance.. 

Elementos

Los elementos de un conjunto realmente pueden ser cualquier cosa: números, estados, automóviles, personas o incluso otros conjuntos son todas las posibilidades para los elementos. Casi todo lo que se pueda recopilar se puede usar para formar un conjunto, aunque hay algunas cosas que debemos tener cuidado.

Conjuntos iguales

Los elementos de un conjunto están en un conjunto o no en un conjunto. Podemos describir un conjunto mediante una propiedad definitoria, o podemos enumerar los elementos en el conjunto. El orden en que se enumeran no es importante. Entonces, los conjuntos 1, 2, 3 y 1, 3, 2 son conjuntos iguales, porque ambos contienen los mismos elementos.

Dos juegos especiales

Dos juegos merecen una mención especial. El primero es el conjunto universal, típicamente denotado U. Este conjunto es todos los elementos que podemos elegir. Este conjunto puede ser diferente de una configuración a la siguiente. Por ejemplo, un conjunto universal puede ser el conjunto de números reales, mientras que para otro problema el conjunto universal puede ser los números enteros 0, 1, 2, .... 

El otro conjunto que requiere atención se llama conjunto vacío. El conjunto vacío es el conjunto único es el conjunto sin elementos. Podemos escribir esto como y denotar este conjunto con el símbolo ∅.

Subconjuntos y el conjunto de potencia

Una colección de algunos de los elementos de un conjunto. UN se llama un subconjunto de UN. Nosotros decimos eso UN es un subconjunto de si si y solo si cada elemento de UN es también un elemento de si. Si hay un número finito norte de elementos en un conjunto, entonces hay un total de 2^norte subconjuntos de UN. Esta colección de todos los subconjuntos de UN es un conjunto que se llama el conjunto de potencia de UN.

Establecer operaciones

Así como podemos realizar operaciones como la suma: en dos números para obtener un nuevo número, las operaciones de teoría de conjuntos se utilizan para formar un conjunto a partir de otros dos conjuntos. Hay varias operaciones, pero casi todas se componen de las siguientes tres operaciones:

• Unión: una unión significa una reunión. La unión de los conjuntos. UN y si consiste en los elementos que están en UN o si.
• Intersección: una intersección es donde se encuentran dos cosas. La intersección de los conjuntos. UN y si consiste en los elementos que en ambos UN y si.
• Complemento: el complemento del conjunto UN consiste en todos los elementos del conjunto universal que no son elementos de UN.

Diagramas de Venn

Una herramienta que es útil para representar la relación entre diferentes conjuntos se llama diagrama de Venn. Un rectángulo representa el conjunto universal para nuestro problema. Cada conjunto se representa con un círculo. Si los círculos se superponen entre sí, esto ilustra la intersección de nuestros dos conjuntos. 

Aplicaciones de la teoría de conjuntos

La teoría de conjuntos se usa en todas las matemáticas. Se utiliza como base para muchos subcampos de las matemáticas. En las áreas relacionadas con las estadísticas, se usa particularmente en probabilidad. Gran parte de los conceptos de probabilidad se derivan de las consecuencias de la teoría de conjuntos. De hecho, una forma de establecer los axiomas de probabilidad implica la teoría de conjuntos.