¿Qué son las cercas internas y externas?

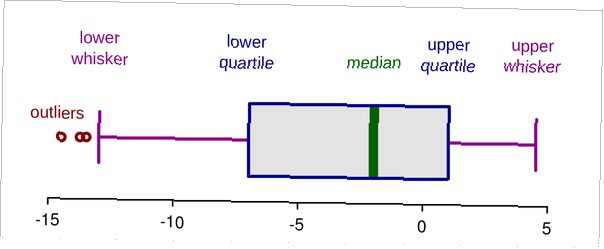
Una característica de un conjunto de datos que es importante determinar es si contiene valores atípicos. Los valores atípicos se consideran intuitivamente como valores en nuestro conjunto de datos que difieren mucho de la mayoría del resto de los datos. Por supuesto, esta comprensión de los valores atípicos es ambigua. Para ser considerado como un valor atípico, ¿cuánto debe desviarse el valor del resto de los datos? ¿Lo que un investigador llama un valor atípico va a coincidir con el de otro? Para proporcionar cierta coherencia y una medida cuantitativa para la determinación de valores atípicos, utilizamos cercas internas y externas.

Para encontrar las cercas internas y externas de un conjunto de datos, primero necesitamos algunas otras estadísticas descriptivas. Comenzaremos calculando cuartiles. Esto conducirá al rango intercuartil. Finalmente, con estos cálculos detrás de nosotros, podremos determinar las cercas interior y exterior..

Cuartiles

El primer y tercer cuartiles son parte del resumen de cinco números de cualquier conjunto de datos cuantitativos. Comenzamos por encontrar la mediana o el punto medio de los datos después de que todos los valores se enumeran en orden ascendente. Los valores inferiores a la mediana corresponden aproximadamente a la mitad de los datos. Encontramos la mediana de esta mitad del conjunto de datos, y este es el primer cuartil.

De manera similar, ahora consideramos la mitad superior del conjunto de datos. Si encontramos la mediana para esta mitad de los datos, entonces tenemos los terceros cuartiles. Estos cuartiles obtienen su nombre del hecho de que dividen el conjunto de datos en cuatro porciones o cuartos de igual tamaño. En otras palabras, aproximadamente el 25% de todos los valores de datos son menores que el primer cuartil. De manera similar, aproximadamente el 75% de los valores de los datos son menores que el tercer cuartil.

Rango intercuartil

Luego necesitamos encontrar el rango intercuartil (IQR). Esto es más fácil de calcular que el primer cuartil q₁ y el tercer cuartil q₃. Todo lo que necesitamos hacer es tomar la diferencia de estos dos cuartiles. Esto nos da la fórmula:

IQR = Q₃ - Q₁

El IQR nos dice cuán extendida está la mitad media de nuestro conjunto de datos.

Encuentra las cercas interiores

Ahora podemos encontrar las cercas interiores. Comenzamos con el IQR y multiplicamos este número por 1.5. Luego restamos este número del primer cuartil. También agregamos este número al tercer cuartil. Estos dos números forman nuestra cerca interior.

Encuentra las cercas exteriores

Para las cercas externas, comenzamos con el IQR y multiplicamos este número por 3. Luego restamos este número del primer cuartil y lo sumamos al tercer cuartil. Estos dos números son nuestras cercas exteriores.

Detectar valores atípicos

La detección de valores atípicos ahora se vuelve tan fácil como determinar dónde se encuentran los valores de datos en referencia a nuestras cercas internas y externas. Si un solo valor de datos es más extremo que cualquiera de nuestras cercas externas, entonces este es un valor atípico y, a veces, se lo conoce como un valor atípico fuerte. Si nuestro valor de datos está entre una cerca interna y externa correspondiente, entonces este valor es un valor atípico sospechoso o un valor atípico leve. Veremos cómo funciona esto con el siguiente ejemplo.

Ejemplo

Supongamos que hemos calculado el primer y tercer cuartil de nuestros datos, y hemos encontrado estos valores en 50 y 60, respectivamente. El rango intercuartil IQR = 60 - 50 = 10. Luego, vemos que 1.5 x IQR = 15. Esto significa que las cercas internas están en 50 - 15 = 35 y 60 + 15 = 75. Esto es 1.5 x IQR menor que el primer cuartil y más del tercer cuartil.

Ahora calculamos 3 x IQR y vemos que esto es 3 x 10 = 30. Las cercas exteriores son 3 x IQR más extremas que el primer y tercer cuartiles. Esto significa que las cercas exteriores son 50-30 = 20 y 60 + 30 = 90.

Cualquier valor de datos que sea menor que 20 o mayor que 90, se consideran valores atípicos. Cualquier valor de datos que esté entre 29 y 35 o entre 75 y 90 se sospecha de valores atípicos..