La regla del complemento

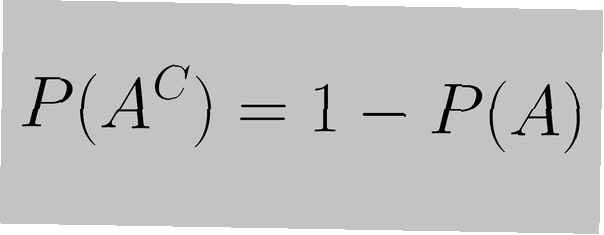
En estadística, la regla del complemento es un teorema que proporciona una conexión entre la probabilidad de un evento y la probabilidad del complemento del evento de tal manera que si conocemos una de estas probabilidades, entonces automáticamente conoceremos la otra..

La regla del complemento es útil cuando calculamos ciertas probabilidades. Muchas veces la probabilidad de un evento es desordenada o complicada de calcular, mientras que la probabilidad de su complemento es mucho más simple.

Antes de ver cómo se usa la regla del complemento, definiremos específicamente qué es esta regla. Comenzamos con un poco de notación. El complemento del evento. UN, que consiste en todos los elementos en el espacio muestral S que no son elementos del conjunto UN, se denota por UNC.

Declaración de la regla del complemento

La regla del complemento se establece como "la suma de la probabilidad de un evento y la probabilidad de su complemento es igual a 1", como se expresa en la siguiente ecuación:

PAG(UN^C) = 1 - P (UN)

El siguiente ejemplo mostrará cómo usar la regla del complemento. Se hará evidente que este teorema acelerará y simplificará los cálculos de probabilidad.

Probabilidad sin la regla del complemento

Supongamos que lanzamos ocho monedas justas: ¿cuál es la probabilidad de que tengamos al menos una cara? Una forma de resolver esto es calcular las siguientes probabilidades. El denominador de cada uno se explica por el hecho de que hay 2⁸ = 256 resultados, cada uno de ellos igualmente probable. Todo esto nos sigue una fórmula para combinaciones:

• La probabilidad de voltear exactamente una cabeza es C (8,1) / 256 = 8/256.
• La probabilidad de voltear exactamente dos cabezas es C (8,2) / 256 = 28/256.
• La probabilidad de voltear exactamente tres cabezas es C (8,3) / 256 = 56/256.
• La probabilidad de voltear exactamente cuatro cabezas es C (8,4) / 256 = 70/256.
• La probabilidad de voltear exactamente cinco cabezas es C (8,5) / 256 = 56/256.
• La probabilidad de voltear exactamente seis cabezas es C (8,6) / 256 = 28/256.
• La probabilidad de voltear exactamente siete cabezas es C (8,7) / 256 = 8/256.
• La probabilidad de voltear exactamente ocho cabezas es C (8,8) / 256 = 1/256.

Estos son eventos mutuamente excluyentes, por lo que sumamos las probabilidades juntas usando una regla de suma apropiada. Esto significa que la probabilidad de que tengamos al menos una cabeza es 255 de 256.

Uso de la regla del complemento para simplificar los problemas de probabilidad

Ahora calculamos la misma probabilidad usando la regla del complemento. El complemento del evento "Volteamos al menos una cabeza" es el evento "No hay cabezas". Hay una forma de que esto ocurra, dándonos la probabilidad de 1/256. Usamos la regla del complemento y encontramos que nuestra probabilidad deseada es uno menos uno de 256, que es igual a 255 de 256.

Este ejemplo demuestra no solo la utilidad sino también el poder de la regla del complemento. Aunque no hay nada malo con nuestro cálculo original, estuvo bastante involucrado y requirió múltiples pasos. Por el contrario, cuando utilizamos la regla del complemento para este problema, no hubo tantos pasos donde los cálculos pudieran salir mal.