¿Qué son los residuos?
 Share
Share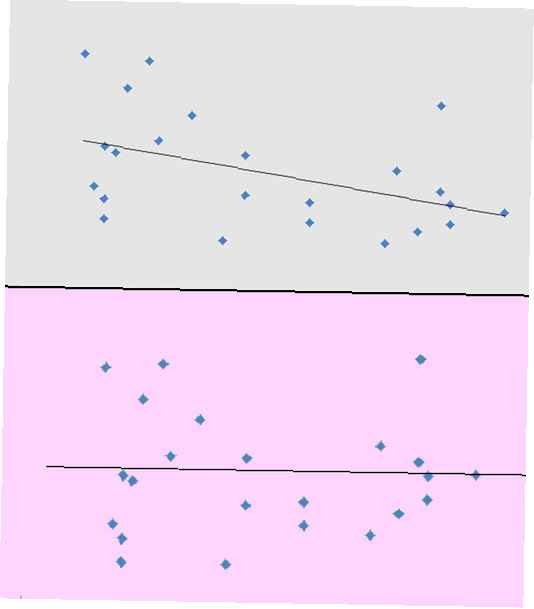
La regresión lineal es una herramienta estadística que determina qué tan bien una línea recta se ajusta a un conjunto de datos emparejados. La línea recta que mejor se ajusta a esos datos se llama la línea de regresión de mínimos cuadrados. Esta línea se puede usar de varias maneras. Uno de estos usos es estimar el valor de una variable de respuesta para un valor dado de una variable explicativa. Relacionado con esta idea está la de un residuo.
Los residuos se obtienen realizando sustracciones. Todo lo que debemos hacer es restar el valor predicho de y del valor observado de y para un particular X. El resultado se llama residual.
Fórmula para residuos
La fórmula para los residuos es sencilla:
Residual = observado y - predicho y
Es importante tener en cuenta que el valor predicho proviene de nuestra línea de regresión. El valor observado proviene de nuestro conjunto de datos..
Ejemplos
Ilustraremos el uso de esta fórmula mediante el uso de un ejemplo. Supongamos que se nos da el siguiente conjunto de datos emparejados:
(1, 2), (2, 3), (3, 7), (3, 6), (4, 9), (5, 9)
Al usar software podemos ver que la línea de regresión de mínimos cuadrados es y = 2X. Usaremos esto para predecir valores para cada valor de X.
Por ejemplo, cuando X = 5 vemos que 2 (5) = 10. Esto nos da el punto a lo largo de nuestra línea de regresión que tiene un X coordenada de 5.
Para calcular el residual en los puntos X = 5, restamos el valor predicho de nuestro valor observado. Desde el y la coordenada de nuestro punto de datos fue 9, esto da un residuo de 9-10 = -1.
En la siguiente tabla vemos cómo calcular todos nuestros residuos para este conjunto de datos:
| X | Y observado | Previsto y | Residual |
| 1 | 2 | 2 | 0 0 |
| 2 | 3 | 4 4 | -1 |
| 3 | 7 7 | 6 6 | 1 |
| 3 | 6 6 | 6 6 | 0 0 |
| 4 4 | 9 9 | 8 | 1 |
| 5 5 | 9 9 | 10 | -1 |
Características de los residuos
Ahora que hemos visto un ejemplo, hay algunas características de los residuos a tener en cuenta:
- Los residuos son positivos para los puntos que están por encima de la línea de regresión..
- Los residuos son negativos para los puntos que caen por debajo de la línea de regresión.
- Los residuos son cero para los puntos que caen exactamente a lo largo de la línea de regresión.
- Cuanto mayor sea el valor absoluto del residual, más lejos estará el punto de la línea de regresión.
- La suma de todos los residuos debe ser cero. En la práctica, a veces esta suma no es exactamente cero. La razón de esta discrepancia es que pueden acumularse errores de redondeo.
Usos de los residuos
Hay varios usos para los residuos. Un uso es ayudarnos a determinar si tenemos un conjunto de datos que tiene una tendencia lineal general, o si deberíamos considerar un modelo diferente. La razón de esto es que los residuos ayudan a amplificar cualquier patrón no lineal en nuestros datos. Lo que puede ser difícil de ver al observar un diagrama de dispersión se puede observar más fácilmente al examinar los residuos y un gráfico de residuos correspondiente.
Otra razón para considerar los residuos es verificar que se cumplen las condiciones de inferencia para la regresión lineal. Después de la verificación de una tendencia lineal (verificando los residuos), también verificamos la distribución de los residuos. Para poder realizar una inferencia de regresión, queremos que los residuos alrededor de nuestra línea de regresión se distribuyan aproximadamente de manera normal. Un histograma o stemplot de los residuos ayudará a verificar que se haya cumplido esta condición..
