Atajo de fórmula de suma de cuadrados

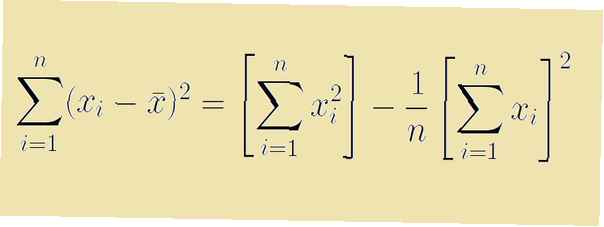
El cálculo de una varianza muestral o desviación estándar generalmente se expresa como una fracción. El numerador de esta fracción implica una suma de desviaciones al cuadrado de la media. En estadística, la fórmula para esta suma total de cuadrados es

Σ (x_yo - X)²

Aquí el símbolo x̄ se refiere a la media de la muestra, y el símbolo Σ nos dice que sumemos las diferencias al cuadrado (x_yo - x̄) para todos yo.

Si bien esta fórmula funciona para los cálculos, existe una fórmula de acceso directo equivalente que no requiere que primero calculemos la media de la muestra. Esta fórmula de acceso directo para la suma de cuadrados es

Σ (x_yo²) - (Σ x_yo)²/ /norte

Aquí la variable norte se refiere al número de puntos de datos en nuestra muestra.

Ejemplo de fórmula estándar

Para ver cómo funciona esta fórmula de acceso directo, consideraremos un ejemplo que se calcula utilizando ambas fórmulas. Supongamos que nuestra muestra es 2, 4, 6, 8. La media de la muestra es (2 + 4 + 6 + 8) / 4 = 20/4 = 5. Ahora calculamos la diferencia de cada punto de datos con la media 5.

• 2 - 5 = -3
• 4 - 5 = -1
• 6 - 5 = 1
• 8 - 5 = 3

Ahora cuadramos cada uno de estos números y los sumamos. (-3)² + (-1)² + 1² + 3² = 9 + 1 + 1 + 9 = 20.

Ejemplo de fórmula de acceso directo

Ahora usaremos el mismo conjunto de datos: 2, 4, 6, 8, con la fórmula de acceso directo para determinar la suma de los cuadrados. Primero cuadramos cada punto de datos y los sumamos: 2² + 4 4² + 6 6² + 8² = 4 + 16 + 36 + 64 = 120.

El siguiente paso es sumar todos los datos y cuadrar esta suma: (2 + 4 + 6 + 8)² = 400. Dividimos esto por el número de puntos de datos para obtener 400/4 = 100.

Ahora restamos este número de 120. Esto nos da que la suma de las desviaciones al cuadrado es 20. Este fue exactamente el número que ya hemos encontrado de la otra fórmula.

Como funciona esto?

Muchas personas simplemente aceptarán la fórmula al pie de la letra y no tienen idea de por qué funciona. Al usar un poco de álgebra, podemos ver por qué esta fórmula de acceso directo es equivalente a la forma tradicional estándar de calcular la suma de las desviaciones al cuadrado.

Aunque puede haber cientos, si no miles de valores en un conjunto de datos del mundo real, asumiremos que solo hay tres valores de datos: x₁ , X₂, X₃. Lo que vemos aquí podría expandirse a un conjunto de datos que tiene miles de puntos.

Comenzamos notando que (x₁ + X₂ + X₃) = 3 x̄. La expresión Σ (x_yo - X)² = (x₁ - X)² + (X₂ - X)² + (X₃ - X)².