Cálculos de distribución de Excel estándar y normal

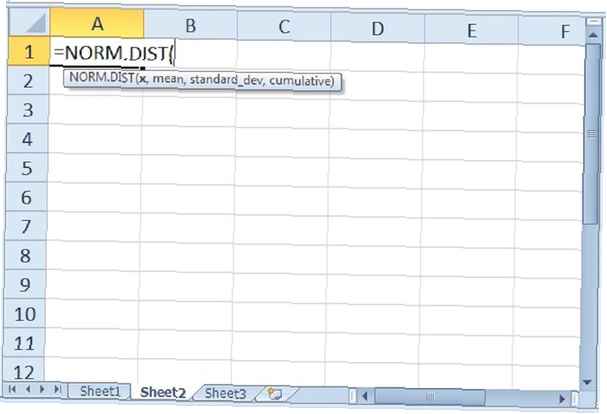
Casi cualquier paquete de software estadístico puede usarse para cálculos relacionados con una distribución normal, más comúnmente conocida como curva de campana. Excel está equipado con una multitud de tablas y fórmulas estadísticas, y es bastante sencillo usar una de sus funciones para una distribución normal. Veremos cómo usar las funciones NORM.DIST y NORM.S.DIST en Excel.

Distribuciones normales

Hay un número infinito de distribuciones normales. Una distribución normal se define por una función particular en la que se han determinado dos valores: la media y la desviación estándar. La media es cualquier número real que indica el centro de la distribución. La desviación estándar es un número real positivo que mide la extensión de la distribución. Una vez que conocemos los valores de la media y la desviación estándar, la distribución normal particular que estamos usando ha sido completamente determinada.

La distribución normal estándar es una distribución especial del número infinito de distribuciones normales. La distribución normal estándar tiene una media de 0 y una desviación estándar de 1. Cualquier distribución normal puede estandarizarse a la distribución normal estándar mediante una fórmula simple. Es por eso que, por lo general, la única distribución normal con valores de tabla es la de la distribución normal estándar. Este tipo de tabla a veces se denomina tabla de puntuaciones z.

NORM.S.DIST

La primera función de Excel que examinaremos es la función NORM.S.DIST. Esta función devuelve la distribución normal estándar. Hay dos argumentos necesarios para la función: "z"Y" acumulativo ". El primer argumento de z es el número de desviaciones estándar de la media. Entonces, z = -1.5 es una desviación estándar y media por debajo de la media. los z-puntuación de z = 2 es dos desviaciones estándar por encima de la media.

El segundo argumento es el de "acumulativo". Hay dos valores posibles que se pueden ingresar aquí: 0 para el valor de la función de densidad de probabilidad y 1 para el valor de la función de distribución acumulativa. Para determinar el área debajo de la curva, querremos ingresar un 1 aquí.

Ejemplo

Para ayudar a comprender cómo funciona esta función, veremos un ejemplo. Si hacemos clic en una celda e ingresamos = NORM.S.DIST (.25, 1), después de presionar enter, la celda contendrá el valor 0.5987, que se ha redondeado a cuatro decimales. ¿Qué significa esto? Hay dos interpretaciones. El primero es que el área bajo la curva para z menor o igual que 0.25 es 0.5987. La segunda interpretación es que el 59.87 por ciento del área bajo la curva para la distribución normal estándar ocurre cuando z es menor o igual a 0.25.

NORM.DIST

La segunda función de Excel que veremos es la función NORM.DIST. Esta función devuelve la distribución normal para una desviación estándar y media especificada. Hay cuatro argumentos necesarios para la función: "X,"" Media "," desviación estándar "y" acumulativo ". El primer argumento de X es el valor observado de nuestra distribución. La media y la desviación estándar se explican por sí mismas. El último argumento de "acumulativo" es idéntico al de la función NORM.S.DIST.

Ejemplo

Para ayudar a comprender cómo funciona esta función, veremos un ejemplo. Si hacemos clic en una celda e ingresamos = NORM.DIST (9, 6, 12, 1), después de presionar enter, la celda contendrá el valor 0.5987, que se ha redondeado a cuatro decimales. Qué significa esto?

Los valores de los argumentos nos dicen que estamos trabajando con la distribución normal que tiene una media de 6 y una desviación estándar de 12. Estamos tratando de determinar qué porcentaje de la distribución ocurre para X menor o igual que 9. De manera equivalente, queremos el área bajo la curva de esta distribución normal particular y a la izquierda de la línea vertical X = 9.

NORM.S.DIST vs NORM.DIST

Hay un par de cosas a tener en cuenta en los cálculos anteriores. Vemos que el resultado para cada uno de estos cálculos fue idéntico. Esto se debe a que 9 es 0.25 desviaciones estándar por encima de la media de 6. Podríamos haber convertido primero X = 9 en un z-puntaje de 0.25, pero el software hace esto por nosotros.

La otra cosa a tener en cuenta es que realmente no necesitamos ambas fórmulas. NORM.S.DIST es un caso especial de NORM.SDIST. Si dejamos que la media sea igual a 0 y la desviación estándar igual a 1, entonces los cálculos para NORM.DIST coinciden con los de NORM.S.DIST. Por ejemplo, NORM.DIST (2, 0, 1, 1) = NORM.S.DIST (2, 1).