Introducción a la función Delta de Dirac

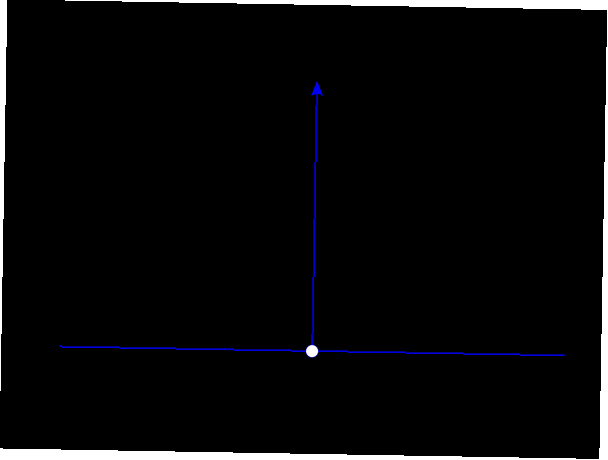
La función delta de Dirac es el nombre dado a una estructura matemática que pretende representar un objeto puntual idealizado, como una masa puntual o una carga puntual. Tiene amplias aplicaciones dentro de la mecánica cuántica y el resto de la física cuántica, ya que generalmente se usa dentro de la función de onda cuántica. La función delta se representa con el símbolo delta en minúscula griega, escrita como una función: δ (X).

Cómo funciona la función Delta

Esta representación se logra al definir la función delta de Dirac de modo que tenga un valor de 0 en todas partes excepto en el valor de entrada de 0. En ese punto, representa un pico que es infinitamente alto. La integral tomada en toda la línea es igual a 1. Si ha estudiado cálculo, es probable que se haya encontrado con este fenómeno antes. Tenga en cuenta que este es un concepto que normalmente se presenta a los estudiantes después de años de estudios universitarios en física teórica..

En otras palabras, los resultados son los siguientes para la función delta más básica δ (X), con una variable unidimensional X, para algunos valores de entrada aleatorios:

• δ (5) = 0
• δ (-20) = 0
• δ (38,4) = 0
• δ (-12,2) = 0
• δ (0,11) = 0
• δ (0) = ∞

Puede escalar la función multiplicándola por una constante. Según las reglas del cálculo, la multiplicación por un valor constante también aumentará el valor de la integral por ese factor constante. Como la integral de δ (X) en todos los números reales es 1, luego multiplicarlo por una constante de tendría una nueva integral igual a esa constante. Entonces, por ejemplo, 27δ (X) tiene una integral en todos los números reales de 27.

Otra cosa útil a tener en cuenta es que, dado que la función tiene un valor distinto de cero solo para una entrada de 0, si está mirando una cuadrícula de coordenadas donde su punto no está alineado en 0, esto puede representarse con una expresión dentro de la entrada de la función. Entonces, si quieres representar la idea de que la partícula está en una posición X = 5, entonces escribirías la función delta de Dirac como δ (x - 5) = ∞ [ya que δ (5 - 5) = ∞]. 

Si luego desea utilizar esta función para representar una serie de partículas puntuales dentro de un sistema cuántico, puede hacerlo sumando varias funciones dirac delta. Para un ejemplo concreto, una función con puntos en x = 5 yx = 8 podría representarse como δ (x - 5) + δ (x - 8). Si luego tomara una integral de esta función sobre todos los números, obtendría una integral que representa números reales, a pesar de que las funciones son 0 en todas las ubicaciones que no sean las dos donde hay puntos. Este concepto se puede ampliar para representar un espacio con dos o tres dimensiones (en lugar del caso unidimensional que utilicé en mis ejemplos).

Esta es una breve introducción a un tema muy complejo. La clave para darse cuenta al respecto es que la función delta de Dirac básicamente existe con el único propósito de hacer que la integración de la función tenga sentido. Cuando no se lleva a cabo una integral, la presencia de la función delta de Dirac no es particularmente útil. Pero en física, cuando se trata de ir desde una región sin partículas que de repente existen en un solo punto, es bastante útil.

Fuente de la función Delta

En su libro de 1930, Principios de la mecánica cuántica, El físico teórico inglés Paul Dirac expuso los elementos clave de la mecánica cuántica, incluida la notación de corchetes y también su función delta de Dirac. Estos se convirtieron en conceptos estándar en el campo de la mecánica cuántica dentro de la ecuación de Schrodinger.